
이번 포스팅에서는 이전에 포스팅하였던 지도학습(Supervised Learning)의 학습 과정에 대해서 좀 더 구체적으로 정리를 해보고자 한다.
지도학습(Supervised Learning) 학습과정 3단계
1단계 데이터 수집 및 특징 추출하기
머신러닝의 지도학습 유형에서는 (X,Y)에서 output에 해당하는 Y(labeling data)가 필요하다. 이 labeling data는 CrowdSourcing을 통하여 labeling 작업이 되고 있다.
input에 해당하는 X의 경우에는 feature의 표현으로, 주어진 X가 어떤식으로 표현이 될 것인가에 대해 결정을 되는 중요한 부분이다.
2단계 ML Model 선택하기
ML Model의 종류로는 아래와 같다.
(1) Logistic regression, SVM : 분류모델
(2) Decision Tree, Random forest : 트리기반, 회귀모델
(3) Nearest neighbor : 비선형 모델 (근처 데이터를 통해 데이터 결정)
(4) Neural Network, MLP : 딥러닝의 모체가 되는 모델
[ML Model 선택 가이드라인]
- 주어진 뎅티터의 특성에 따라 특정 ML Model이 더 낫다는 판단이 있을 수 있다.
- 많은 데이터 분석의 경험을 통해서 상대적으로 데이터가 많다면, Parameter가 많은 모델들이 Parameter가 적은 모델보다는 더 효과적으로 동작할 수 있다.
3단계 파라미터 값 최적화하기
주어진 모델하에서 모델이 가지고 있는 학습하고자하는 Parameter의 값을 결정하는 단계이다.
아래와 같이 회귀(regression)그래프가 주어져있고, 실제 우리가 학습하고자하는 Parameter값들이 아래와 같이 분포되어있다고 가정하자.
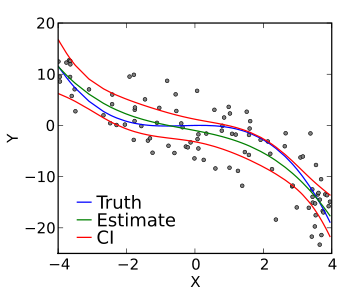
f(x; w1, w2, w3)에서 각 각의 가중치 w1, w2, w3 값을 조정해서 우리가 학습하고자 하는 Parameter값들을 좀 더 잘 표현 할 수 있는 모델을 결정지을 수 있도록 조정할 수 있다. 하지만 첨부한 사진에서 보듯이 정성적 판단(사람의 눈으로 판단)으로만 본다면 명확히 어느 가중치의 값이 가장 최적의 값인지 알 수 없다.
따라서 이 경우에는 정량적 판단(지표를 통한 판단)이 중요하다. f(x)와 y간의 관계에서 error를 최소화 함으로써 우리가 학습하고자 하는 Parameter와 실제 데이터 간의 오차범위가 작음을 확인하는 것이다.
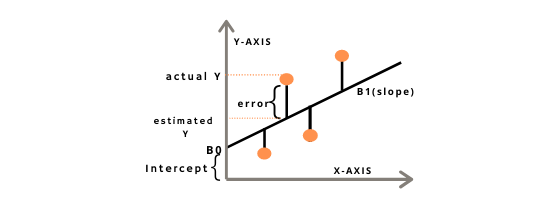
아래의 공식은 에러의 정도를 정량적으로 판단하기위한 것으로, 위의 그래프에서 선형함수(예측값)와 Parameter(실제값) 사이의 차이값(actual Y - estimated Y)의 제곱된 값을 모든 데이터 (x,y)에 대해 모두 시행하여 합한 것을 의미한다. 여기서 W는 Error를 최소화하기 위한 값인데, 이 에러를 최소화시켜줄 값 W를 통해서 최고의 모델을 찾을 수 있다.

주어진 데이터를 표현하는 최고의 Parameter를 찾는 문제는 f(x)와 y사이에서 에러를 최소화 시키는 것이다 이것이 최적화 문제이며, 문제해결에는 아래의 두 가지 방법이 있다.
(1) Analytic solution : 방정식 풀이를 통해 최적의 해 구하기
(2) Numerical solution : 주어진 함수를 통해 해를 구하지 못하는 경우, 수치를 통해 해와 가장 가깡툰 근사치를 구한다
이렇게 학습된 Model을 사용해서 새로운 input x를 통해 output y를 예측하거나 추론한다.