이번 포스팅에서는 이전 포스팅에서 개괄적으로 분류해보았던 Unsupervised Learning에 대해서 좀 더 구체적으로 정리를 해보고자 한다.
Unsupervised Learning ?
Supervised Learning이란 (X(input), Y(output))에서 Y(output) 값에 대한 레이블이 제공되지 않은 상태로, 최소한의 사람의 개입을 통해 데이터를 해석해서 숨겨진 데이터의 패턴을 찾아낸다.
그 예시로 각기 다른 모양과 색상을 가진 사과와 바나나가 나열되어있다고 가정해보자. 어떤 기준으로 나열을 할 것인가? 앞서 이미 언급을 했듯이 Y라는 label이 주어지지 않은 상태에서 기계는 주어진 데이터들을 분류해야한다. 기계는 사람과 같이 직관력이 없기 때문에 모양이 동그란지 혹은 길죽한지에 따라서 분류를 하기도 하고, 색상이 알록달록한지 아닌지에 따라 분류하기도 한다.
Unsupervised Learning 예시
그렇다면 비지도 학습의 예시로는 어떤것들이 있을까?
우선 첫 번째, 클러스터링(lustering)이 있다. Clustering은 Classification과 비슷하지만 Y labeling data가 주어지지 않는다는 점이 다르다. Clustering은 말 그대로 data duples을 clusters로 grouping하는 것을 말한다. Similar/Dissimilar를 정의함에 있어서는 사람이 개입을 하게 되는데, 이 부분에 있어서만 최소한으로 사람이 개입하게 된다.
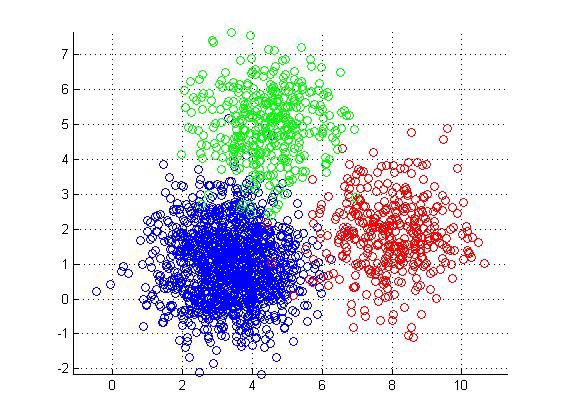
두 번째, 차원축소(Dimensionality reduction)가 있다. 대표적인 예시로 PCA(Principal Component Analysis)가 있으며, 2차원의 데이터를 1차원 데이터로, 3차원 데이터를 2차원 데이터로 축소를 하게 된다. 이렇게 차원을 축소하게 되면 어떤 효과가 있을까?
우선 첫 번째 고차원에서는 알 수 없었던 correlation(상관관계)를 효과적으로 알 수 있고, 불필요한 noise를 제거할 수 있으며, 저장공간을 효율적으로 사용 할 수 있다. 그리고 마지막으로 시각화와 해석능력이 좋아진다.
세 번째, 밀집도 판단(Density estimation) : sample 모양이 규칙적이지 않고, 복잡한 모양인 경우가 많다. 이러한 복잡하고 규칙적이지 않은 모양의 영역에서 실제 데이터 영역을 추출해내야되는 경우가 많은데, 우리는 Manifold Hypothesis라는 용어에 집중해야 한다. 이 용어는 고차원 데이터라 할지라도 실질적으로 해당 데이터를 나타내주는 저차원 공간인 manifold 존재한다는 것을 의미한다. (sparse한 고차원 데이터를 간추려서 보다 저차원 공간으로 나타낼 수 있다는 의미)
manifold란, 다차원 데이터에서 실질적으로 의미를 가지는 특징을 모아둔 조밀한 특성 공간을 뜻하며, 실제 데이터를 통해 스스로 학습하는 딥러닝 비지도 학습이 이러한 manifold를 스스로 찾아낸다.
이러한 Manifold Hypothesis를 통해 가능한 가능해진 기술이 바로 GAN(Generative Adversarial Network)로, 실제로 존재하지 않는 사람을 예상으로 생성해내는 기술이다. 최근에는 사람 이외에도 자연 이미지도 예상/예측해서 생성해내고 있다.
이외에도 style-based GAN, video-to-video synthesis, source to tareget GAN 등이 있다.