210420 결정 알고리즘(Decision algorithm)을 활용한 문제풀이

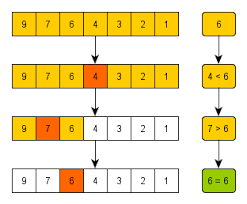
결정 알고리즘은 이분검색을 기반으로 한다.

알고리즘 문제에서 주어진 조건에서의 최대값 혹은 최소값을 구하는 문제 중에 몇 몇 문제는 결정 알고리즘(Decision algorithm)을 활용해서 풀이해야 한다.
결정 알고리즘은 이분 검색을 기반으로 하는 문제로, 전체 데이터를 순회하면 시간 복잡도 O(N)을 갖지만 이분 검색으로 데이터를 검색하면 O(logN)만큼의 시간 복잡도를 갖는다.

예시문제
길이가 N인 숫자 리스트가 있다고 가정했을때, 총 T 개의 그룹으로 리스트를 나눠야 한다.
T개의 그룹으로 리스트를 나눴을때 한 그룹당 최소 얼마의 숫자합이여야 하는지 구하시오.

const numList = [1, 3, 2, 5, 4, 7, 6, 9, 8];
// 숫자 리스트의 최소 합과 최대 합을 구한다.
// 숫자 리스트에서 최대값이 최소합
let lt = Math.max(...numList);
// 숫자 리스트 전체 요소들의 합이 최대합
let rt = numList.reduce((acc, n) => acc + n, 0);
const target = 3;
let answer = 0;

// 총 몇 개의 그룹으로 나눠지는지 판별하는 함수
function count(numList, mid) {
  // 처음 그룹
  let cnt = 1;
  let sum = 0;
  for (let n of numList) {
    // sum + n의 값이 한계값을 초과하는 경우,
    if (sum + n > mid) {
      // 더하는 그룹의 갯수를 1증가
      cnt += 1;
      // 합계를 다음 더할 숫자 n으로 초기화
      sum = n;
    } else {
      // 아직 합계가 한계값을 초과하지 않은 경우,
      // 계속해서 sum에 값 n을 누적한다.
      sum += n;
    }
  }
  return cnt;
}

while (lt <= rt) {
  // 최소합 ~ 최대합의 중간 값부터 탐색을 시작
  let mid = Math.floor((lt + rt) / 2);
  // 조건 그룹 갯수보다 작거나 같은 경우,
  if (count(numList, mid) <= target) {
    // 해당 합계는 answer가 될 수 있는 조건을 충족
    answer = mid;
    // 조건을 만족하기 때문에 mid - 1을 최대 범위로 업데이트
    rt = mid - 1;
  } else {
    // 만약 조건을 만족하지 않은 경우, 최소값을 mid + 1로 업데이트
    lt = mid + 1;
  }
}